Onnittelin heitä oikeasta vastauksesta ja annoin heille kaksi uutta harjoitustehtävää.
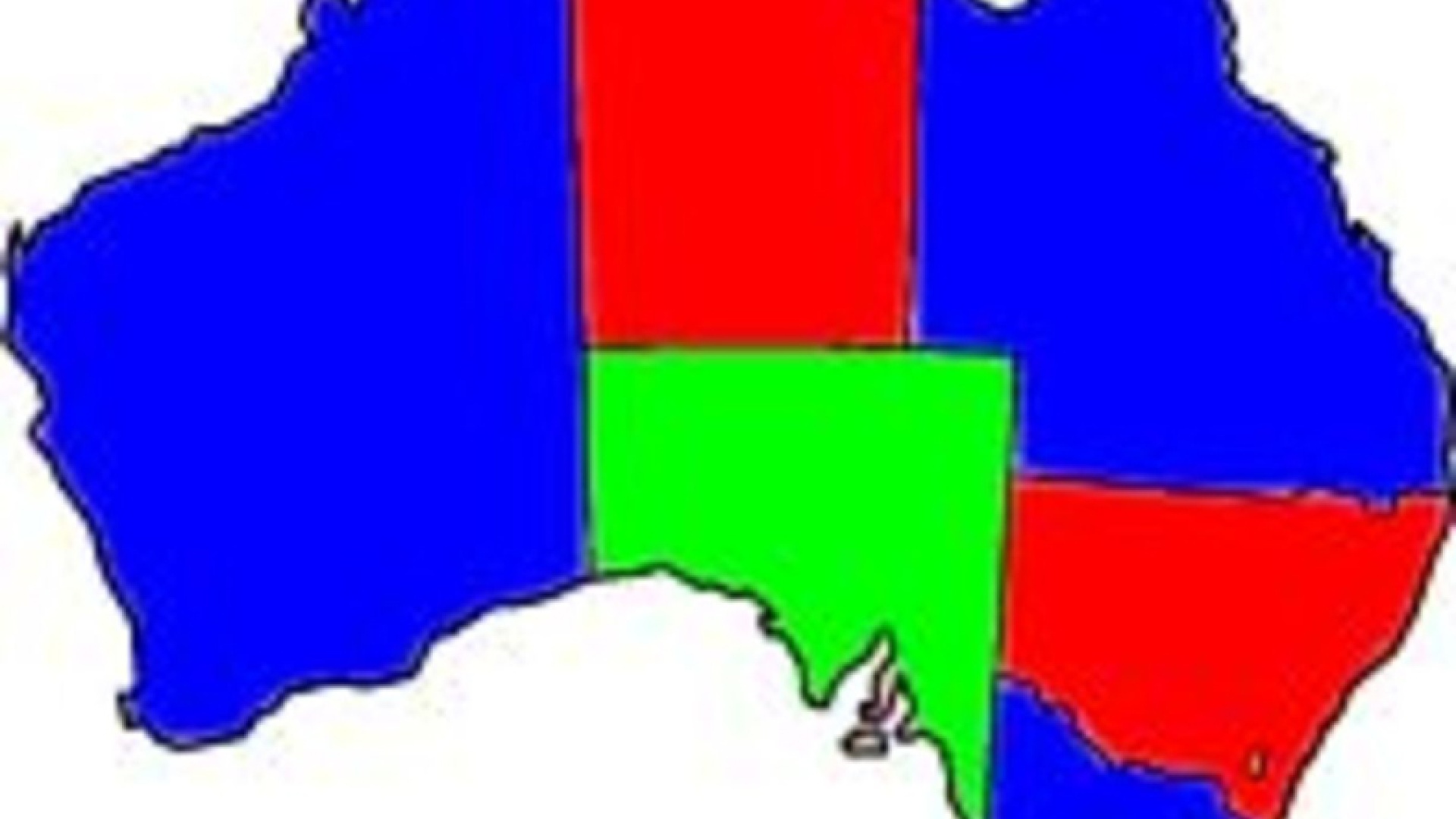
1. Piirtäkää sellainen valtio osavaltioineen, että värejä tarvitaan vähintään neljä. Antakaa piirros sitten vieruskaverillenne ja pyytäkää tätä värittämään se.
2. Piirtäkää toinen valtio, jonka värittämiseen tarvitaan vähintään viisi väriä. Antakaa piirros vieruskaverillenne ja pyytäkää tätä värittämään se.
Oppilailla oli hauskaa heidän keksiessään omia valtioitaan ja nimetessään niitä. Ensimmäisessä tehtävässä oli omat haasteensa, sillä oikea tapa värittää ei ollut aina ihan ilmeinen.
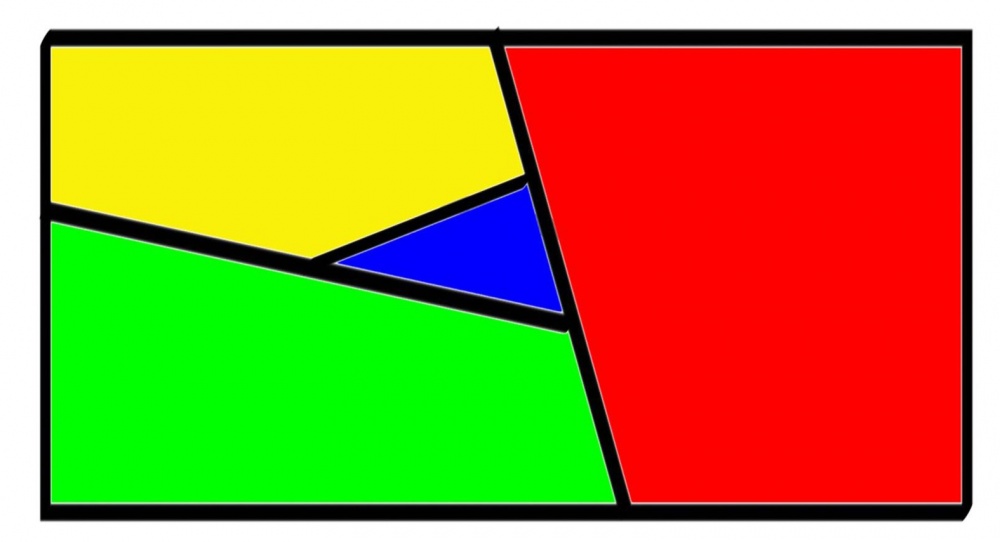
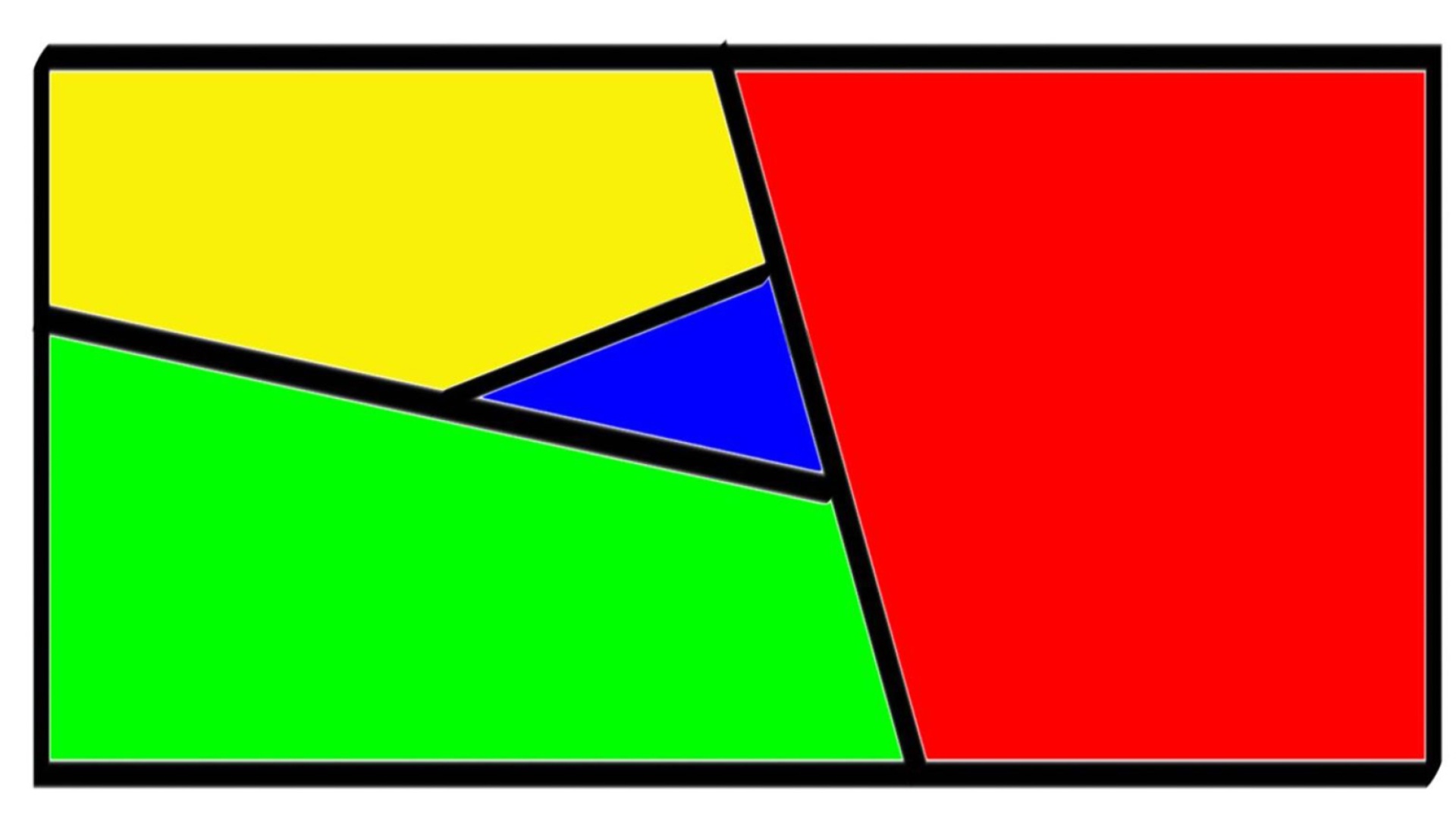
Otsikkokuvassa on yksinkertaisin mahdollinen kartta, jonka värittämiseen tarvitaan neljä väriä.
Toisen tehtävän kanssa kävi juuri niin kuin olin olettanut. Se aiheutti pieniä kiistoja: kävi ilmi, että vaikka värien vähimmäismäärän piti olla viisi, kartat pystyi silti värittämään neljällä värillä.
Yksi kerrallaan kävimme läpi oppilaiden piirtämät kartat ja totesimme, että ne on mahdollista värittää vain neljällä värillä. Mitä ihmettä? Pyysin heitä yrittämään uudelleen – turhaan – ja paljastin heille sitten tunnetun matemaattisen lauseen, neliväriteoreeman:
Jokainen tasokartta voidaan värittää neljällä värillä siten, että kaksi vierekkäistä aluetta ovat aina erivärisiä.
Vaatimuksena on se, että kahden alueen välillä on rajaviiva, pelkkä rajapiste ei riitä tekemään alueista vierekkäisiä.
Kerroin oppilaille, että tässä on todennäköisesti ensimmäinen heidän kohtaamansa esimerkki todellisesta matematiikasta. Matematiikassa on nimittäin kyse ajatuksista, ei aritmetiikasta. Oppilaat halusivat tietää asiasta enemmän.
Kerroin, kuinka vuonna 1852 matemaatikko nimeltä Francis Guthrie väritti Englannin kreivikuntia ja huomasi tarvitsevansa ainoastaan neljää väriä. Hän kertoi havainnostaan veljelleen Frederickille lähettämässään kirjeessä, jonka veli välitti edelleen toiselle matemaatikolle.
Yli sadan vuoden ajan matematiikat yrittivät turhaan todistaa neliväriteoreemaa. Vuonna 1976 Kenneth Appel ja Wolfgang Haken vihdoin onnistuivat tehtävässä.
Kysyin oppilailta, miten teoreeman voisi todistaa oikeaksi. He ehdottivat, että voisimme piirtää kaikki mahdolliset kartat ja värittää ne sitten neljällä värillä. Sain heidät toisiin ajatuksiin toteamalla, että erilaisia karttoja on ääretön määrä.
Miten todistus sitten onnistuisi? Neliväriteoreema oli ensimmäinen merkittävä matemaattinen teoreema, joka todistettiin oikeaksi tietokoneen avulla.
Todistaakseen neliväriteoreeman Appel ja Haken turvautuivat matemaatikoiden suosimaan menetelmään, jonka nimenä on reductio ad absurdum. Se toimii seuraavalla tavalla:
Jos haluamme todistaa jotakin oikeaksi, oletamme, että se ei päde, jolloin matematiikka ei toimi. Olettamalla, että jokin ei ole totta, päädymme ristiriitaan tunnettujen tosiasioiden kanssa. Niinpä alkuperäinen oletus on väärä, joten todistusta kaipaavan väitteen täytyy olla tosi.
Appel ja Haken sovelsivat menetelmää olettamalla, että on olemassa kartta, jonka värittäminen edellyttää viiden värin käyttöä. Sitten he osoittivat, että on olemassa 1936 kartan joukko, josta yksikään ei voi olla osa heidän olettamaansa isompaa karttaa.
Sen jälkeen Appel ja Haken osoittivat, että jokaisen mahdollisen kartan täytyy pitää sisällään yksi näistä pienemmistä kartoista, mikä johti ristiriitaan.
Todistus vaatii suuren määrän tarkistuksia, joten Appel ja Haken laativat tietokoneohjelman, joka teki valtaosan työstä. Niinpä neliväriteoreemasta tuli ensimmäinen tietokoneella todistettu merkittävä matemaattinen teoreema.
Koska todistuksessa oli tietokoneella merkittävä rooli, monet epäilivät sen paikkansapitävyyttä: teoreemaa on käytännössä mahdoton todistaa ”käsin”.
Vuonna 1975 matemaatikko Martin Gardner esitti aprillipilana 110 alueen muodostaman "kartan", joka oli hänen mukaansa mahdoton värittää ainoastaan neljällä värillä. Gardnerin väitteen osoittaminen vääräksi vaati 24 vuotta ja melkoisen määrän tietokoneaikaa.
Silti yhä edelleen jotkut epäilevät neliväriteoreeman pätevyyttä.
Adrian Dudek
Australian National University
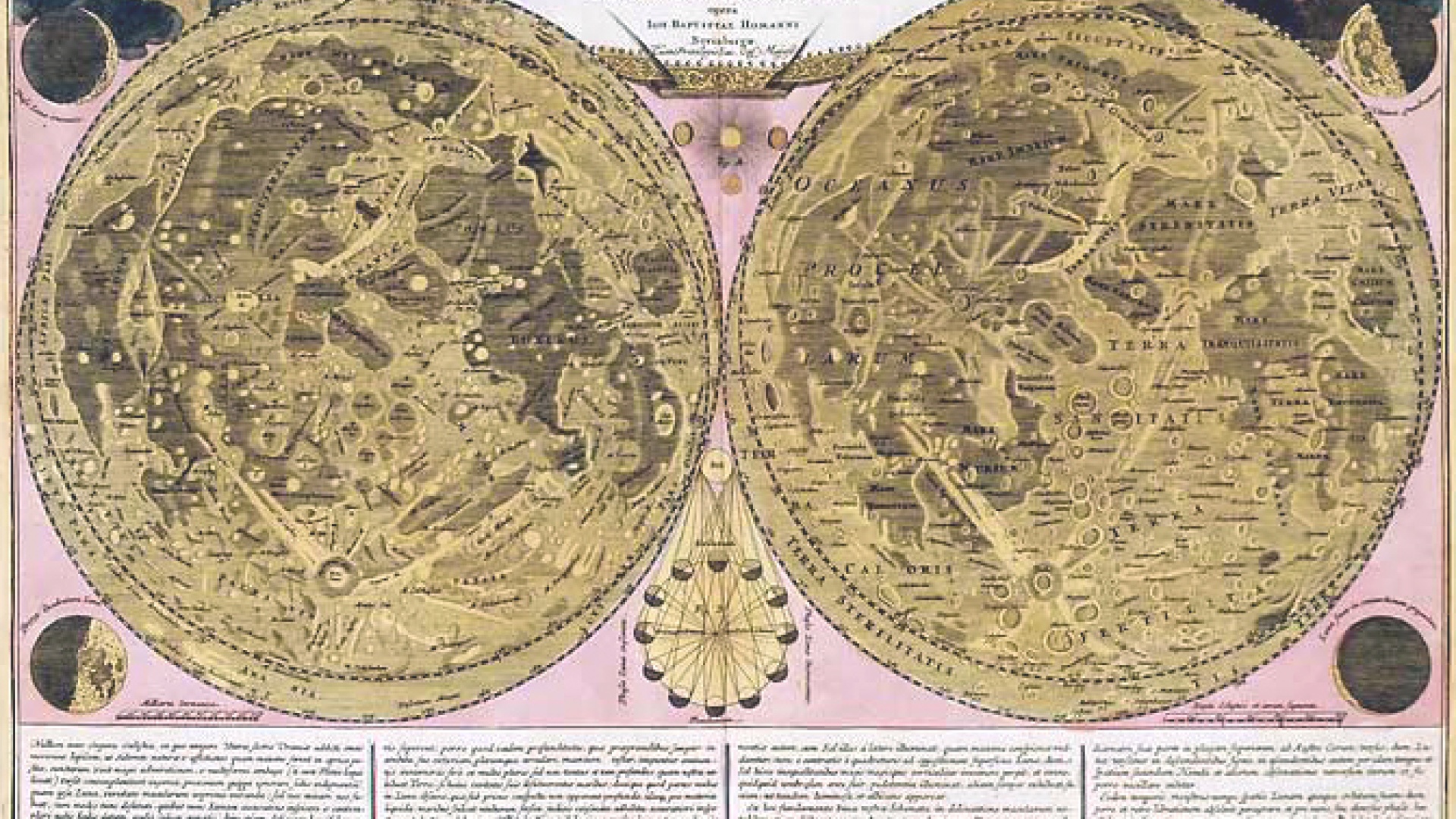
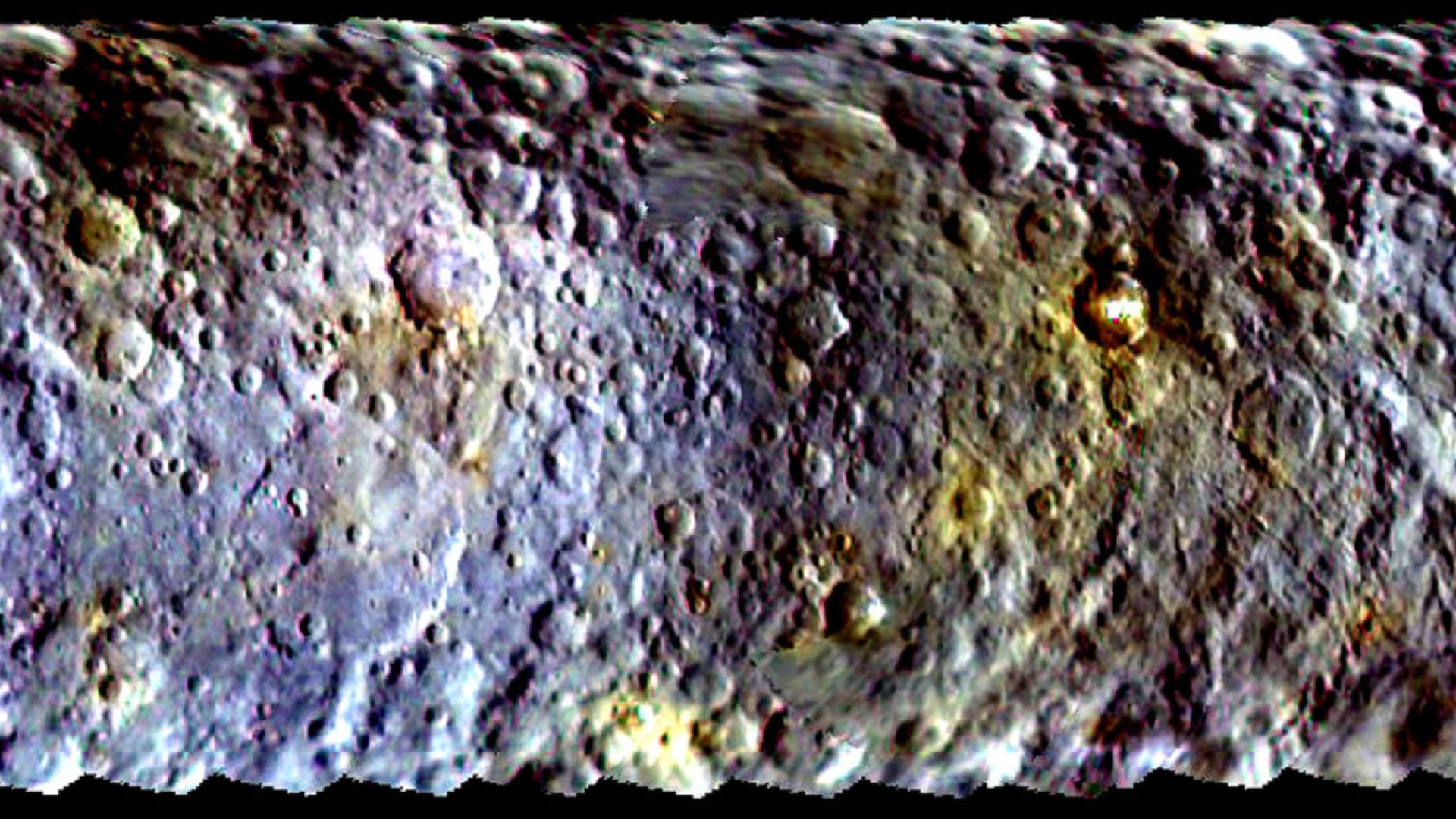
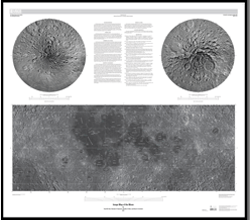 Karttoja on kaksi: Ensimmäinen on laajakulmakameran tasalaatuinen näkymä koko pallon pinnasta (vasemmalla), toinen taas on topografian (Kuun pinnanmuodot) näyttävä kartta (oikealla). Käytännössä nämä kartat ovat nyt parhaiten kalibroituja standardikarttoja mitä naapuristamme on tähän mennessä tehty.
Karttoja on kaksi: Ensimmäinen on laajakulmakameran tasalaatuinen näkymä koko pallon pinnasta (vasemmalla), toinen taas on topografian (Kuun pinnanmuodot) näyttävä kartta (oikealla). Käytännössä nämä kartat ovat nyt parhaiten kalibroituja standardikarttoja mitä naapuristamme on tähän mennessä tehty.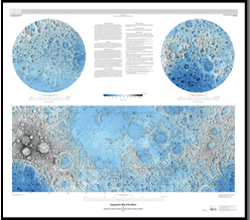 Karttoja selailevan kannattaa muistaa, että niiden mittakaava vaihtelee huomattavasti. Pääkarttojen projektio on Mercator, joka vääristää kokoja huomattavasti. Napojen lähellä taas käytetään polaarista stereografista projekiota.
Karttoja selailevan kannattaa muistaa, että niiden mittakaava vaihtelee huomattavasti. Pääkarttojen projektio on Mercator, joka vääristää kokoja huomattavasti. Napojen lähellä taas käytetään polaarista stereografista projekiota.